1.理解二维卷积和矩阵乘法之间的转换

参考资料：

1. https://www.zhihu.com/question/22298352/answer/34267457
2. http://blog.csdn.net/lingerlanlan/article/details/23863347
3. http://blog.csdn.net/zsz_shsf/article/details/53201669
4. https://en.wikipedia.org/wiki/Toeplitz_matrix
5. 在 Caffe 中如何计算卷积？

卷积神经网络的卷积计算实现是通过矩阵乘法来实现的，为了实现这种计算，需要把其中一个矩阵转换成Toeplitz矩阵

Toeplitz矩阵的概念：

矩阵中每条自左上至右上的斜线上的元素相同，形如：

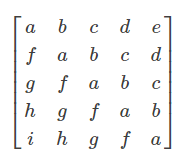
一般形式为：

Toeplitz矩阵具有的一个很特殊的性质：可以用来表示卷积运算

通过上述知识已经能够基本上了解到如何将矩阵卷积转换为矩阵乘法的。

2.CNN神经网络中对于图像卷积的底层实现

参考资料：

1. K. Chellapilla, S. Puri, and P. Simard. High performance convolutional neural networks for document processing. In Proc. ICFHR. Suvisoft, 2006.

参考资料1中的第2节讲述了如何Unroll(展开)卷积操作3.GEMM

参考资料：

1. https://petewarden.com/2015/04/20/why-gemm-is-at-the-heart-of-deep-learning/

General Matrix Matrix Multiply的简称